In industrial piping design – especially for pipes subjected to internal pressure – determining the minimum required wall thickness is a critical step to ensure safety and optimize material usage.
ASME B31.3 – Process Piping specifies several parameters that influence this calculation, among which the Y factor plays a significant role in adjusting the final design thickness.
1. Wall Thickness Calculation per ASME B31.3
According to Equation (3a) in ASME B31.3, the minimum required wall thickness is calculated as follows:
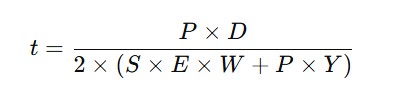
Where:
t = required wall thickness (excluding corrosion allowance)
P = internal design pressure
D = outside diameter
S = allowable stress of the material at design temperature
E = longitudinal weld joint quality factor
W = weld strength reduction factor
Y = coefficient defined in ASME B31.3
In practice, hoop stress within a pipe wall is not uniformly distributed – the inner wall experiences higher stress than the outer wall. In pipe stress analysis, relying solely on the maximum theoretical hoop stress from Lamé’s equation – without applying a correction factor would lead to an overly conservative design, resulting in unnecessary wall thickness, higher fabrication cost, and increased material usage.
The Y factor is introduced to:
- Simplify calculations for thin-wall piping without resorting to complex thick-wall pressure equations.
- Optimize the design by ensuring both safety and cost-efficiency.
- More accurately represent the actual stress state by accounting for stress redistribution after localized yielding.
Under internal pressure, the inner wall experiences the peak hoop stress and is the first to undergo localized plastic deformation. However, this does not lead to immediate failure; instead, it allows stress redistribution across the wall thickness.
Because the actual operating stress becomes lower than the theoretical peak predicted by Lamé, ASME permits using a correction factor Y < 1, reducing the calculated wall thickness while still maintaining compliance and safety.
2. Origin of the Y Factor – Lamé’s Hoop Stress Equation
The basis for pipe wall thickness calculations comes from Lamé’s hoop stress equation, which describes the stress distribution across the wall of a pressurized cylinder:
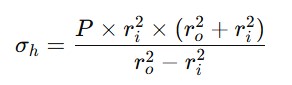
Where:
σₕ = hoop stress at any radial position
P = internal pressure
rᵢ, rₒ = inner and outer radii of the pipe
From this relationship, the hoop stress at the inner radius (rᵢ) is always higher than at the outer radius (rₒ), meaning the stress is non-uniformly distributed. If the design were based solely on this maximum inner-wall stress, the resulting wall thickness would be overly conservative and not material-efficient.
To address this, ASME B31.3 introduces the Y factor to correct the difference between theoretical peak stress and actual redistributed stress, reflecting the material’s ability to redistribute stress after localized yielding.
3. Y-Factor Values in ASME B31.3
According to the tables in the code, the Y factor for certain materials increases with temperature. This means ASME B31.3 allows greater flexibility in wall-thickness calculations at elevated temperatures, where the material’s mechanical properties change.
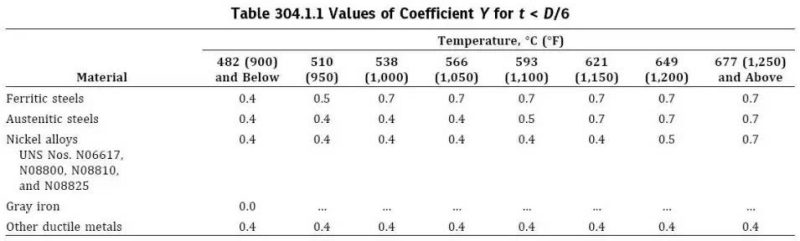
As temperature rises, the material becomes more ductile and capable of better stress redistribution → Y increases → required wall thickness decreases.
For gray cast iron, Y = 0 because the material is brittle and lacks ductility, making it prone to sudden fracture—therefore the code does not permit any reduction in thickness.
For ductile non-ferrous metals (e.g., copper, aluminum), Y remains constant at all temperatures, since these materials are inherently soft and capable of effective stress redistribution.
Translation and reference source: https://whatispiping.com/importance-of-y-factor-asme-b31-3/
