Phân tích phần tử hữu hạn (FEA) được ứng dụng rộng rãi để tính toán và phân tích cho nhiều thiết bị công nghiệp, trong đó bao gồm các thiết bị áp lực như nồi hơi, bình chứa và hệ thống đường ống. Các thiết bị này phải chịu áp suất lớn và điều kiện vận hành khắc nghiệt, do đó đảm bảo an toàn và độ bền là ưu tiên hàng đầu. FEA cho phép các kỹ sư mô phỏng chính xác ứng suất của thiết bị dưới áp lực, nhiệt độ và các yếu tố liên quan đến vận hành khác.
Trong thiết kế nồi hơi & bình bồn áp lực, đường ống,…FEA được dùng để kiểm tra độ bền của các chi tiết chịu nhiệt và áp lực, đảm bảo rằng vật liệu không bị phá hủy trong quá trình vận hành.
FEA giúp phát hiện điểm yếu trong thiết kế, tối ưu hóa cấu trúc, giảm chi phí sản xuất và tăng hệ số an toàn, mang đến giải pháp hiệu quả cho các doanh nghiệp trong ngành công nghiệp nặng.
1. Giới thiệu chung về phân tích phần tử hữu hạn (FEA)
1.1. Định nghĩa FEA
Phân Tích Phần Tử Hữu Hạn (Finite Element Analysis – FEA) là một kỹ thuật số hóa để giải quyết các vấn đề cơ học phức tạp trong thiết kế kỹ thuật. Phương pháp này chia nhỏ một cấu trúc lớn thành các phần tử nhỏ (elements) và mô hình hóa sự biến đổi của các phần tử này dưới tác động của lực, ứng suất, và điều kiện biên. Qua việc phân tích các tương tác giữa các phần tử, FEA cho phép dự đoán ứng suất, biến dạng, và các yếu tố khác trong hệ thống.
1.2. Vai trò quan trọng của FEA trong quy trình thiết kế sản phẩm
FEA giữ vai trò thiết yếu trong quy trình thiết kế sản phẩm hiện đại, giúp kỹ sư phát hiện các điểm yếu cục bộ trước khi đưa vào chế tạo. Bằng cách mô phỏng các điều kiện thực tế, FEA cung cấp thông tin chính xác về hiệu suất và độ bền của sản phẩm, từ đó hỗ trợ thiết kế và tối ưu hóa. Điều này không chỉ giúp rút ngắn thời gian đưa sản phẩm ra thị trường mà còn giúp giảm thiểu chi phí phát triển sản phẩm.

1.3. So sánh FEA với các phương pháp phân tích truyền thống khác
Khác với các phương pháp phân tích truyền thống tính toán theo công thức, phương pháp phân tích tay hoặc mô hình hóa đơn giản, FEA cho phép xử lý các cấu trúc phức tạp với độ chính xác cao hơn. Các phương pháp truyền thống thường dựa vào các công thức và ước lượng, dẫn đến khả năng dư thừa, sai số lớn trong các tình huống không đơn giản. Trong khi đó, FEA có khả năng tính toán đa biến và áp dụng các điều kiện biên phức tạp, cung cấp một cái nhìn chi tiết và toàn diện hơn về biến đổi của cấu trúc. Điều này đã khiến FEA trở thành một công cụ quan trọng trong thiết kế kỹ thuật và phân tích cấu trúc hiện đại.
2. Nguyên lý hoạt động của Phân tích phần tử hữu hạn
Phân tích Phần tử Hữu hạn (FEA) là một phương pháp số học mạnh mẽ được sử dụng trong kỹ thuật để mô phỏng và dự đoán cách các kết cấu và hệ thống biến đổi dưới các điều kiện cụ thể. Bằng cách phân chia kết cấu phức tạp thành những phần tử nhỏ hơn và dễ quản lý hơn, FEA cho phép các kỹ sư tính toán chi tiết các yếu tố như độ bền, độ cứng và biến dạng của vật liệu, nhằm tối ưu hóa thiết kế và đảm bảo an toàn cho sản phẩm.
Nguyên lý chính của FEA là phân chia chi tiết quan tâm thành các phần tử nhỏ, hay còn gọi là “meshing”, sau đó liên kết các phương trình vật lý tương ứng để giải quyết bài toán kỹ thuật. Phương pháp này được ứng dụng rộng rãi trong nhiều lĩnh vực, từ công nghiệp ô tô, hàng không, lò hơi, thiết bị áp lực, kết cấu thép đến kỹ thuật dân dụng, cho phép các kỹ sư dự đoán hành vi của hệ thống trước khi sản xuất hoặc xây dựng, từ đó tối ưu hóa và giảm thiểu chi phí thử nghiệm thực tế.
Nguồn: tham khảo
3. Quy trình Phân tích phần tử hữu hạn (FEA)
FEA bao gồm ba giai đoạn chính: tiền xử lý (pre-process), xử lý (process), và hậu xử lý (post-process). Mỗi giai đoạn đều đóng vai trò quan trọng trong việc mô phỏng các vấn đề kỹ thuật thực tế và cung cấp kết quả chính xác cho quá trình phân tích và thiết kế.
3.1. Tiền xử lý (Pre-process)
Trong giai đoạn tiền xử lý, các kỹ sư cần xác định các thông số vật lý và điều kiện thực tế áp dụng cho mô hình phân tích. Điều này bao gồm việc mô tả hình học của đối tượng, xác định các tính chất vật liệu và điều kiện biên.
- Mô tả hình học: Đối tượng cần phân tích, chẳng hạn như khung ô tô hoặc cánh máy bay, vách lò hơi, vỏ bồn áp lực, đường ống sẽ được xác định hình học thông qua các phần mềm CAD (Computer-Aided Design). Mô hình này sẽ trở thành nền tảng cho các bước tiếp theo của FEA.
- Tính chất vật liệu: Các thuộc tính của vật liệu, như độ cứng, độ bền, và khả năng chịu nhiệt,…sẽ được cung cấp vào hệ thống. Các tính chất này ảnh hưởng trực tiếp đến cách đối tượng phản ứng với các điều kiện môi trường hoặc tải trọng áp đặt.
- Điều kiện biên và tải trọng: Điều kiện biên có thể là các yếu tố bên ngoài như lực, nhiệt độ, hoặc áp suất mà đối tượng sẽ phải chịu đựng trong suốt quá trình hoạt động. Xác định chính xác các yếu tố này rất quan trọng để mô phỏng thực tế đúng với những gì xảy ra trong điều kiện hoạt động thực tế.
3.2. Xử lý (Process)
Giai đoạn này là trung tâm của quá trình phân tích FEA, nơi đối tượng sẽ được chia thành các phần tử nhỏ và áp dụng các phương trình vật lý phù hợp.
- Chia lưới (Meshing): Đối tượng được chia thành các phần tử nhỏ hơn, mỗi phần tử có hình dạng đơn giản (ví dụ, hình tam giác hoặc hình tứ giác). Các phần tử này cùng với các điểm nút (nodes) kết nối chúng lại với nhau, tạo thành một hệ thống các phần tử mà thông qua đó các phương trình vật lý sẽ được giải. Meshing là bước vô cùng quan trọng vì độ chi tiết và độ chính xác của lưới phần tử sẽ ảnh hưởng trực tiếp đến kết quả phân tích. Độ dày của lưới phải phù hợp với độ phức tạp của đối tượng: các vùng phức tạp hơn yêu cầu lưới dày hơn, trong khi các vùng ít phúc tạp hơn có thể có lưới thô hơn.
- Áp dụng phương trình vật lý: Sau khi chia lưới, các phương trình vật lý được áp dụng cho từng phần tử. Các phương trình này có thể liên quan đến cơ học, nhiệt học, hoặc thậm chí từ trường, tùy thuộc vào loại vấn đề cần giải quyết.
Ở đây, hệ thống các phương trình đại số tuyến tính được lắp ráp dựa trên phương trình vật lý cơ bản như phương trình cân bằng động lực học hoặc phương trình nhiệt động lực học. Sau đó, hệ thống phương trình này sẽ được giải thông qua các phương pháp số học để cung cấp thông tin về phản ứng của vật liệu dưới các điều kiện đã xác định.
3.3. Hậu xử lý (Post-process)
Giai đoạn cuối cùng của quy trình FEA là phân tích kết quả và rút ra kết luận từ mô hình đã tính toán.
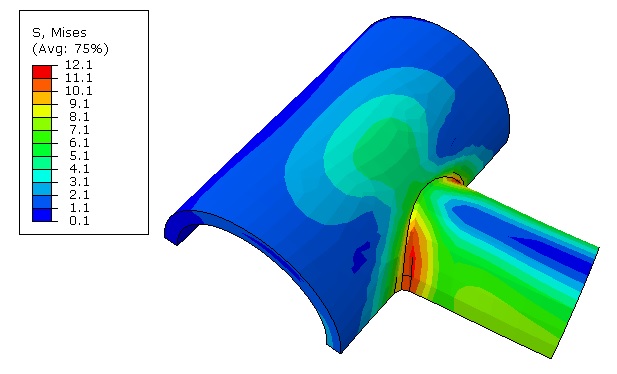
- Kết quả mô phỏng: Kết quả có thể là các biểu đồ, hình ảnh, hoặc dữ liệu số thể hiện các biến như biến dạng, ứng suất, hay nhiệt độ trong cấu trúc. Các kỹ sư sử dụng kết quả này để xác định những điểm yếu, điểm quá tải hoặc các vấn đề tiềm ẩn trong thiết kế.
- Phân tích kết quả: Kết quả của FEA không chỉ giúp kiểm tra thiết kế có chịu được tải trọng hay không mà còn hỗ trợ tối ưu hóa thiết kế. Kỹ sư có thể thực hiện các điều chỉnh cần thiết để cải thiện hiệu suất hoặc giảm trọng lượng, chi phí sản phẩm.

Nếu kết quả cho thấy đối tượng không đạt yêu cầu, các kỹ sư sẽ quay lại các bước trước đó, điều chỉnh chiều dày, vật liệu, lưới phần tử, phương trình vật lý hoặc điều kiện biên cho phù hợp, rồi lặp lại quy trình phân tích.
4. Ứng dụng của phân tích phần tử hữu hạn FEA
4.1. Phân tích ứng suất
Xác định các vùng chịu ứng suất lớn nhất: FEA giúp xác định các khu vực mà ứng suất cao nhất xảy ra trong cấu trúc, từ đó giúp các kỹ sư thiết kế các yếu tố gia cố hoặc điều chỉnh hình dáng để giảm thiểu nguy cơ hư hỏng.
Đánh giá độ bền của sản phẩm: Bằng cách mô phỏng các điều kiện hoạt động thực tế, FEA cung cấp thông tin về khả năng chịu đựng của sản phẩm trước các tải trọng.
4.2. Phân tích biến dạng
Dự đoán độ biến dạng của sản phẩm dưới tác dụng của tải trọng: FEA cho phép dự đoán cách mà sản phẩm sẽ biến dạng khi chịu tải trọng, giúp tối ưu hóa thiết kế.
Kiểm tra khả năng chịu tải của cấu trúc: Các kỹ sư có thể kiểm tra xem cấu trúc có đủ khả năng chịu tải hay không và điều chỉnh nếu cần.
4.3. Phân tích nhiệt
Tính toán phân bố nhiệt độ trong sản phẩm: FEA có thể mô phỏng sự phân bố nhiệt trong cấu trúc để đảm bảo sản phẩm hoạt động hiệu quả trong các điều kiện nhiệt độ khác nhau.
Đánh giá hiệu quả tản nhiệt: Giúp xác định liệu thiết kế có đủ khả năng tản nhiệt trong quá trình hoạt động hay không.
4.4. Phân tích động
Mô phỏng các hiện tượng rung động, va chạm: FEA cho phép đánh giá cách mà sản phẩm sẽ thay đổi dưới tác động của rung động hoặc va chạm, đảm bảo tính ổn định và an toàn của sản phẩm.
Đảm bảo độ ổn định của sản phẩm: Các bài toán động lực học có thể được phân tích để đảm bảo rằng sản phẩm có thể hoạt động ổn định trong mọi điều kiện.
4.5. Ứng dụng khác
Ngoài các ứng dụng nêu trên, FEA còn được sử dụng trong các lĩnh vực như:
- Phân tích mỏi: Đánh giá khả năng chịu đựng của vật liệu dưới tác động của tải trọng lặp đi lặp lại.
- Phân tích nứt: Kiểm tra và mô phỏng sự phát triển của các vết nứt trong cấu trúc.
- Phân tích dòng chảy: Đánh giá cách mà chất lỏng hoặc khí di chuyển qua cấu trúc, điều này rất quan trọng trong các ứng dụng như thiết kế ống dẫn, bể chứa, và các thiết bị nhiệt.
